Entre las dificultades conceptuales que se hace necesario abordar para la correcta evaluación del movimiento de fondos, probablemente la más crítica, y de uso práctico más generalizado, sea la que se designa por valor cronológico del dinero.
El origen del concepto valor cronológico del dinero arranca de la premisa de que el dinero tiene un coste de utilización significativo. Este coste de utilización presenta un doble sentido:
- O bien es necesario desembolsar intereses por su utilización, si nos ha sido prestado.
- O bien presenta un coste de oportunidad equivalente a los intereses que nos pagarían y que dejamos de percibir.
Por tanto, dado un cierto capital, caben dos alternativas:
- Disponer de él, en cuyo caso incurrimos en un coste de oportunidad.
- Ceder su uso durante uno o más períodos de tiempo, en este caso, dicho capital devengará unos intereses que constituyen la compensación económica por la falta de disponibilidad del capital durante el intervalo de tiempo que se cede.
Habitualmente, se trabaja con una tasa de interés que se expresa en tanto por ciento, o por uno, del capital durante el intervalo de tiempo que se cede.
La generación de intereses por un capital se designará por capitalización. Bajo un régimen de capitalización compuesta, al capital inicial se le acumulan periódicamente los intereses devengados en dicho periodo, siendo el principal, así obtenido, el nuevo capital inicial que produce intereses durante el siguiente período.
Por consiguiente, en términos matemáticos sencillos, si C0 es el capital inicial prestado e i el interés en tanto por uno y referido al periodo de tiempo que se considere, al final del primer periodo el capital disponible C1 será:
C1 = C0 + C0 * i = C0 (1+i)
Y al final del segundo período, tendremos:
C1 = C0 + C0 * i = (1+i) = C0 (1+i) (1+i) = C0 (1+i) 2
Demostrada la recurrencia, o por inducción, el capital Cn disponible al final del periodo n será:
Cn = Co (1+i)n
Como se verá, además de su interés general, las expresiones anteriores servirán de base, en epígrafes sucesivos, para el cálculo de la rentabilidad de la inversión.
Al factor (1+i)n se le denomina factor de capitalización compuestas para un período enésimo.
La expresión gráfica del anterior desarrollo matemático, vendrá dado por la figura:
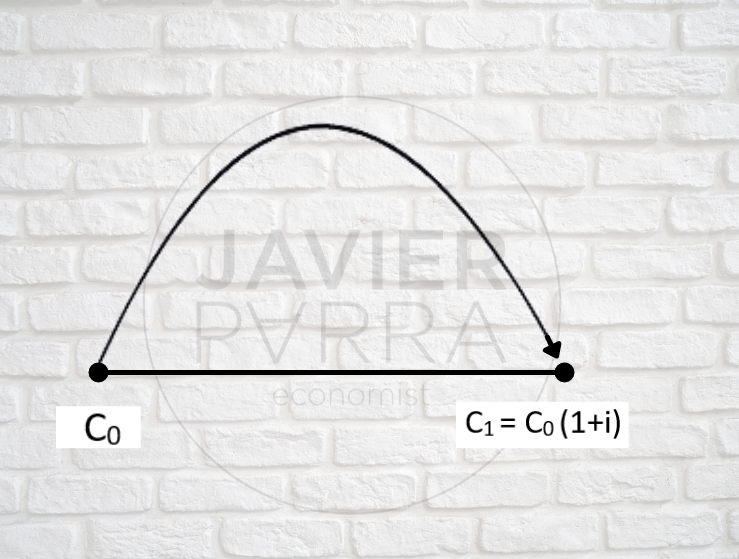
C0 equivalente a Ci al cabo de un período.
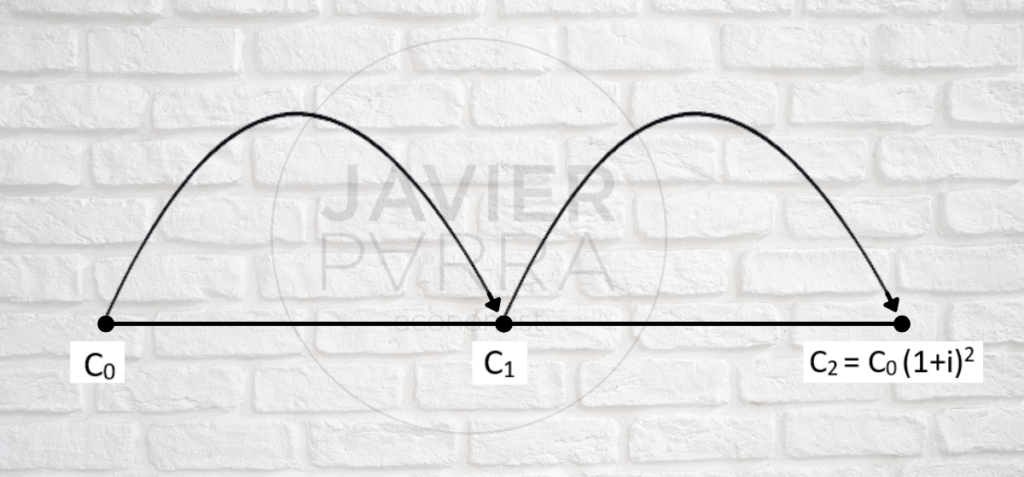
C0 equivale a C2 al cabo de dos períodos.
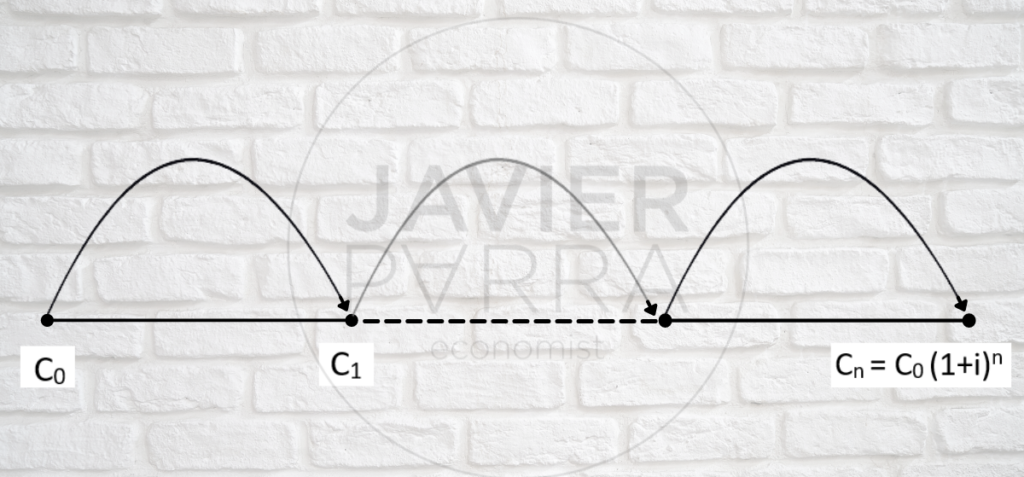
C0 equivale a Cn al cabo de n períodos.
La operación inversa a la capitalización se denomina actualización, y consiste en función de un capital Cn con vencimiento en el período n, calcular el capital C0 con vencimiento en el periodo 0 que lo produjo, para ello bastará con despejar de la ecuación general de capitalización compuesta.
Cn = C0 (1+i)n
La incógnita C0, con lo que obtenemos.
C0 = Cn (1+i)-1
Que de manera gráfica será:
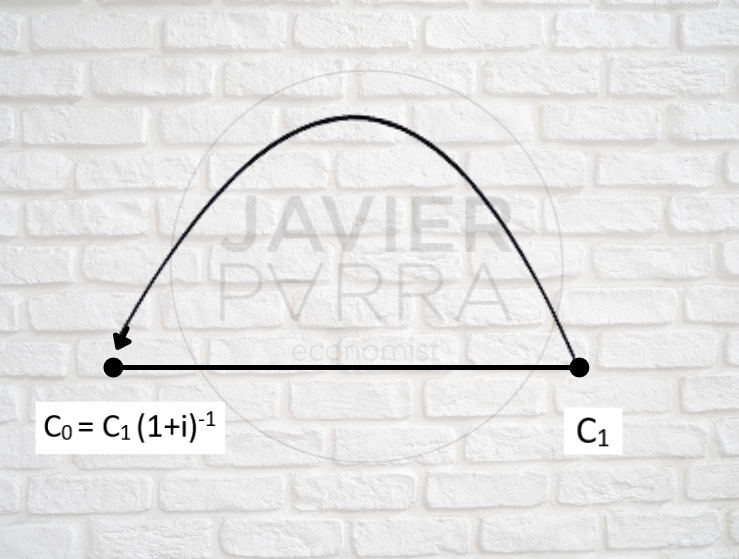
El valor actual de C1 es C0
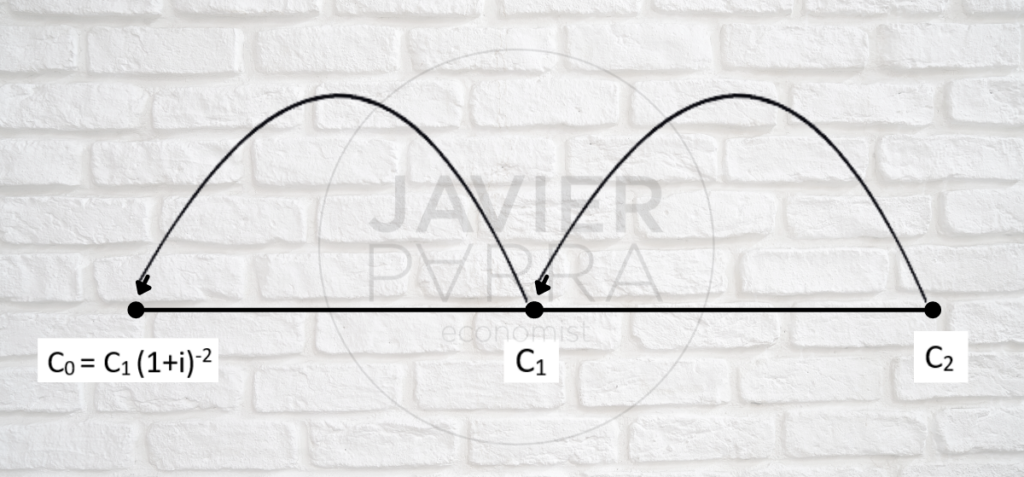
El valor actual de C2 es C0
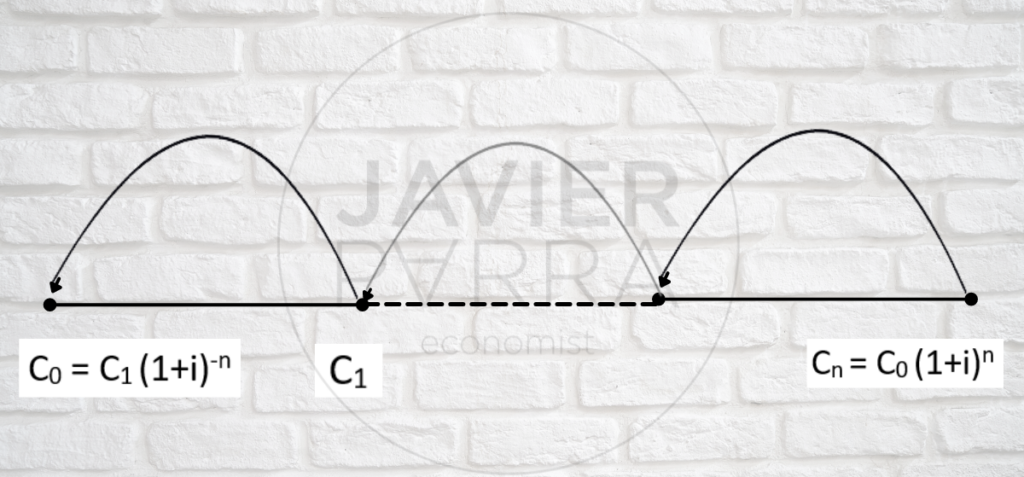
El valor actual de Cn es C0
De manera similar a la operación de capitalización, el factor (1+i)-n se denomina factor de actualización para un período enésimo.
Finalmente y por ser un equívoco muy generalizado, vamos a destacar las diferencias entre valor cronológico y valor adquisitivo del dinero.
El valor cronológico del dinero se refiere a que C1 vale más que C0 , porque C1 > C0 en unidades de igual valor adquisitivo.








