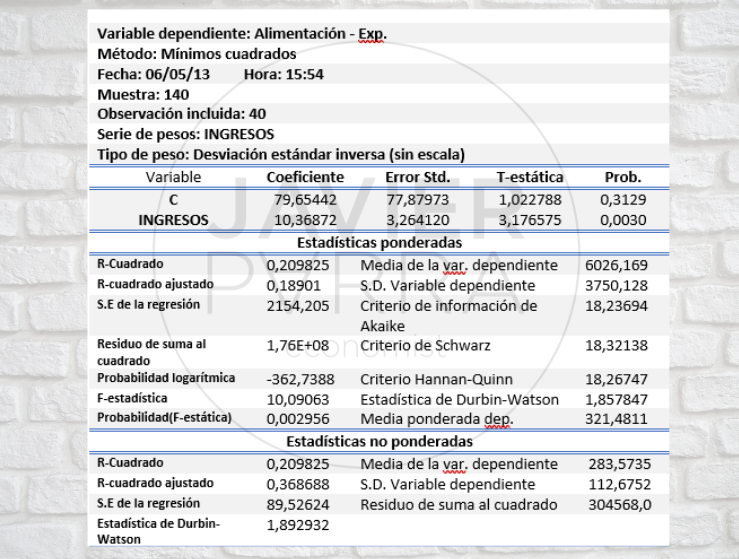
En la detección de heterocedasticidad influyen diversos factores como:
A- Parcelas residuales
- Estimación del modelo utilizando los mínimos cuadrados y trazos del residuo de los mínimos cuadrados.
- Con más de una variable explicativa, se grafica el residuo de mínimos cuadrados contra cada variable explicativa, para ver si esos residuos varían de forma sistemática en relación con la variable especificada.
- OLS en el modelo transformado es de mínimos cuadrados ponderados (MCP)
- ¿Por qué el MCP es más eficiente que el OLS en el modelo original?
- Las observaciones con una gran varianza son menos informativas que las observaciones con una pequeña varianza y, por lo tanto, deben tener menos peso.
- MCP es un es un caso especial de mínimos cuadrados generalizados (MCG)
B- La prueba Goldfeld-Quandt
- Hipótesis nula H0: σ21 =σ22 =σ2
- Se obtienen las estimaciones (σ21) del Modelo 1 y (σ22) del Modelo 2 aplicando los mínimos cuadrados por separado al primer y al segundo grupo de observaciones.
Modelo de rendimiento de los cultivos
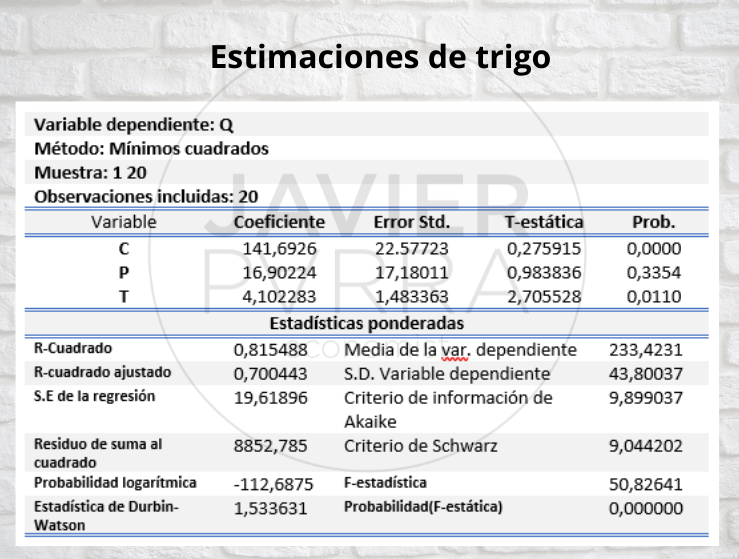
- Q es el rendimiento de la muestra por acre plantado
- P es el precio
- T es la tecnología
Las fuentes potenciales de heteroscedasticidad pueden ser los cambios en la tecnología, los programas gubernamentales y las variables climatológicas o las semillas transgénicas. La mayoría de los programas de mejora incrementan la resistencia a las enfermedades. Los rendimientos de los cultivos serían menos variables a medida que mejora la resistencia a las enfermedades.