Para hablar de una introducción a la econometría es preciso establecer fundamentos matemáticos y estadísticos que permitan la comprensión de la misma. Partiendo del sumatorio:
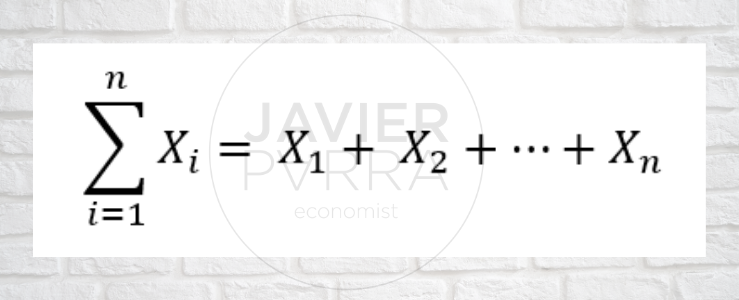
- El símbolo Σ es la letra griega mayúscula sigma y significa «la suma de».
- La letra i se llama índice de suma, esta letra es arbitraria y puede aparecer también como t, j o k.
- La expresión ∑(i=1)^n se lee como la suma de los términos Xn desde i igual a uno hasta n.
- Los números i y n son el límite inferior y el límite superior de la sumatoria.
Reglas de la operación de suma

- Una variable radom es una variable cuyo valor es desconocido hasta que se observa.
- Una variable aleatoria discreta sólo puede tomar un número limitado o contable de valores.
- Una variable aleatoria continua puede tomar cualquier valor en un intervalo.
- La población es el conjunto de individuos que tienen ciertas características y que son de interés para un investigador.
- La muestra es un subconjunto de la población.
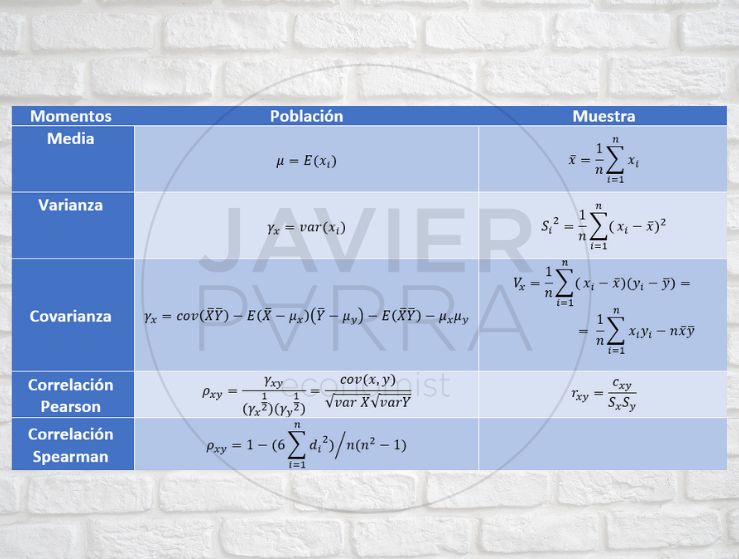
Momentos de la población y muestra
Media de la muestra, valores medios o esperados:
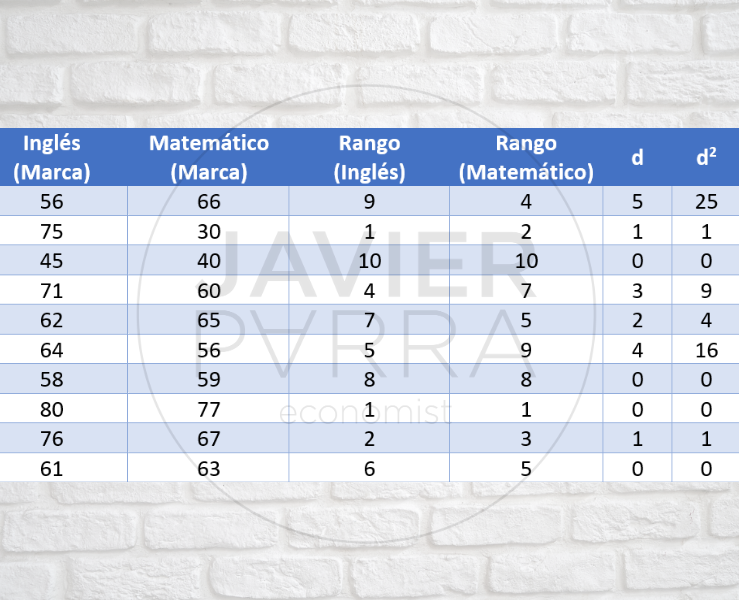
Una relación monótona es una de las siguientes:
- Cuando el valor de una variable aumenta, también lo hace el valor de la otra.
- Cuando el valor de una variable disminuye, el valor de la otra variable disminuye.
Veamos el siguiente el ejemplos de relaciones monótonas y no monótonas:

Valores esperados de las funciones de una variable aleatoria
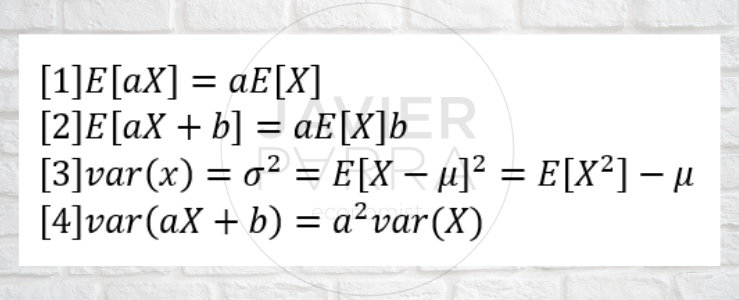
Valores esperados de varias variables aleatorias
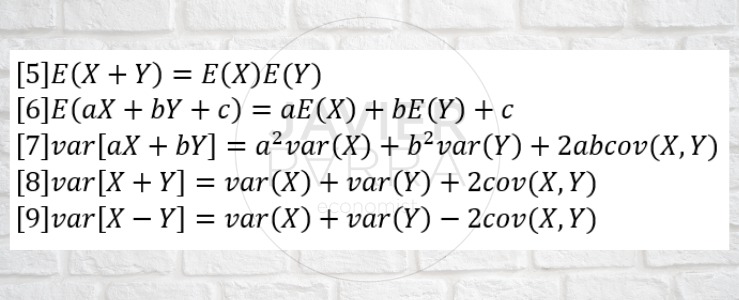
Algunas distribuciones de probabilidad importantes
Normal o gaussiana; si X es una variable aleatoria normalmente distribuida con media 𝝻 y varianza σ2, se puede simbolizar como X~N(𝝻,σ2 )
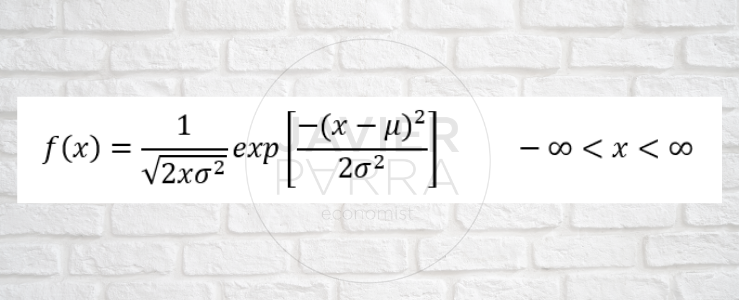
Chi-cuadrado: Si X, es una variable aleatoria normalmente distribuida con media 0 y varianza σ2, entonces V= X12 +X22 +…+Xm2 ~ X(m)2
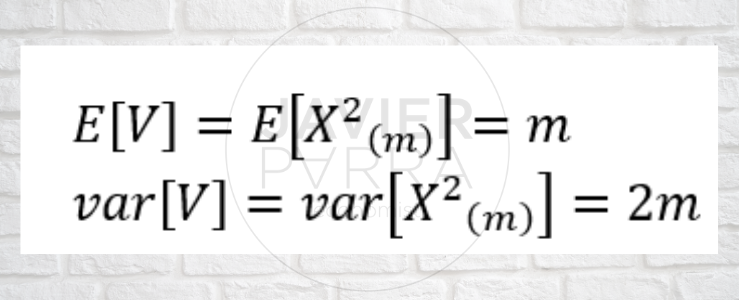
Una variable random de Student se forma dividiendo una variable aleatoria normal estándar con media 0 y varianza 1, por la raíz cuadrada de una variable aleatoria independiente chi-cuadrado, V que ha sido dividida por sus grados de libertad m.







